Recursion is a foundational computer science concept that many concepts are built on top of. Recursion can elegantly solve many algorithms or it can create massive time complexities that ruin your code.
But before jumping into the deep end, let’s start simple.
Recursion is the term for a function calling itself.
Here is a example of a function calling itself
public void Foo()
{
Foo();
}If you run this code, the computer will freeze and give some type of stack overflow error. This happens because of infinite recursion. While this code is mostly useless, when harnessed it can be very powerful.
Why?
Because very similar to a for loop, the code above is iterating. We need a way to stop this code and we can do so with what’s called a base case.
Replacing for loops with recursion
Let’s create a simple countdown function that counts down from 10 to 1.
public void Countdown(int number)
{
for(int i = number; i >= 0; i--)
{
Console.WriteLine(i);
}
}This function works great but let’s swap out the for loop with some recursion:
public void Countdown(int number)
{
Console.WriteLine(number);
CountDown(number - 1);
}As you can see, our solution is not perfect we’ll end up infinitely printing negative numbers. To prevent this from happening we need to end the countdown at 0 and prevent the recursion from going infinite.
public void Countdown(int number)
{
if(number < 0) Console.WriteLine("Recursion stopped");
Console.WriteLine(number);
CountDown(number - 1);
}Recursion Underneath The Hood
To truly understand recursion, we need to understand how a computer itself processes recursion.
Lets say we call our previous function CountDown(10). Since 10 is not less than zero, the computer reaches the line:
CountDown(number - 1);This calls the functions CountDown(9).
But we must ask ourselves a very important question. When the computer begins to run CountDown(9), did the computer complete CountDown(10)?
This is what makes recursion difficult to understand for new programmers. The computer is not technically “done” with CountDown(10) , yet it still calls CountDown(9).
Even more confusing this process continues all the way down to CountDown(1) ! All of these functions are running at once! How is the computer doing this?!
The Call Stack
Computers use a stack to keep track of functions it’s in the middle of calling. The stack is known, appropriately enough, as the call stack.
In our example the computer begins by callingCountDown(10). Before the method completes executing, CountDown(9). In order to track that the computer is still in the process of CountDown(10), the computer pushes that function onto the call stack.

The computer then proceeds to execute CountDown(9). Before the computer can execute CountDown(8) , though, the computer needs to remember that it’s in the middle of CountDown(9).

The computer will then continue this operation till we reach our base case.
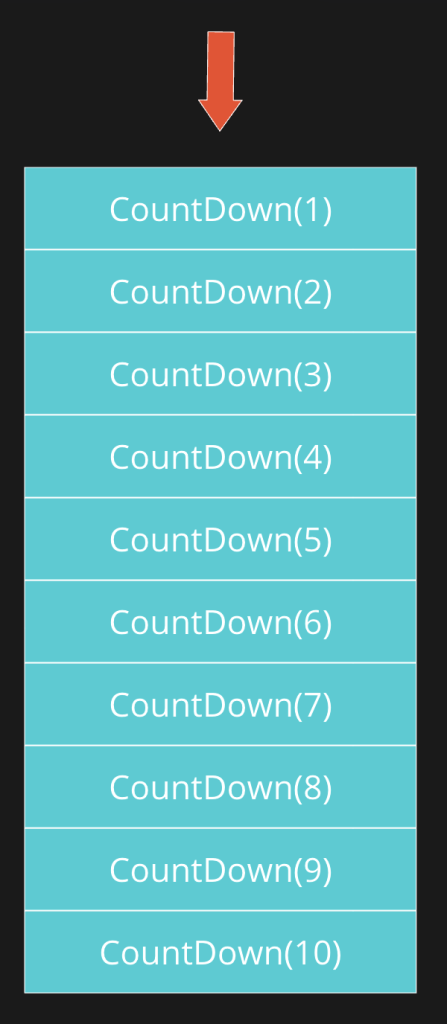
If you remember from Stacks, we can only pop off the its top element. This is great for recursion! We can just pop off the top element off the stack once we get done with everything!
The next thing the computer does is pop the top element off the stack which is CountDown(1).

Real Life Recursion Scenario
One type of problem recursion is great for solving is searching trees. Take the example of traversing a file system.
Lets say that we want to write a simple program that traverses a file system printing all the directories.
public static void FindDirectories(string directory)
{
// Inspect each file within directory
foreach (var filename in Directory.EnumerateFileSystemEntries(directory))
{
// If the current file is itself a subdirectory:
if (Directory.Exists(filename))
{
// Print out the full path name:
Console.WriteLine(filename);
}
}
}This code is great, but what if we want to search directories within our directory? We could add another for loop within our previous for loop.
public static void FindDirectories(string directory)
{
// Loop through first-level directory
foreach (var filename in Directory.EnumerateFileSystemEntries(directory))
{
if (Directory.Exists(filename))
{
Console.WriteLine(filename);
// Loop through second-level subdirectory
foreach (var innerFilename in Directory.EnumerateFileSystemEntries(filename))
{
if (Directory.Exists(innerFilename))
{
Console.WriteLine(innerFilename);
}
}
}
}
}Now every time our loop finds a directory it also conducts an identical loop through the subdirectories of that directory.
But what if we wanted to search even further? This is where things begin to get dicey because we have no clue where the directory ends.
And this is where recursion comes to the rescue. With recursion we can write a script that goes to the bottom of the directory and is flexible too.
public static void FindDirectories(string directory)
{
// Inspect each file within the directory. Some of these "files" may
// actually be subdirectories.
foreach (var filename in Directory.EnumerateFileSystemEntries(directory))
{
// If the current file is itself a subdirectory:
if (Directory.Exists(filename))
{
// Print out the full path name:
Console.WriteLine(filename);
// Recursively call this function on the subdirectory
FindDirectories(filename);
}
}
}As the program finds files that are directories, it call the FindDirectories() method upon that very subdirectory. Recursion is great at delving into multiple layers of a problem without knowing how many layers there are.
Turning Any Iteration Into Recursion
Another valuable skill is to take any iterative problem and turn it into recursion. Let’s take an array of integers and square each element.
Since we are using recursion, lets start simple and just create the function.
public void SquareArray(int[] arr)
{
SquareArray(arr);
}Now, we need code to square the integer, but which number do we square? Let’s square the first number:
public void SquareArray(int[] arr)
{
arr[0] *= arr[0];
SquareArray(arr);
}
We have successfully squared the number at index 0, but how do we proceed to square the number at index 1?
Now, if we were to use a loop instead of recursion, we would have used a variable to keep track of the index and continuously increased it by 1.
public void SquareArray(int[] arr)
{
for(int i = 0; i < arr.Length; i++)
{
arr[0] *= arr[0];
}
}We have one issue with the recursive version. The only argument the function can take is the array. We need some way to keep track of and increment an index.
We can essentially add extra state to our recursive function by passing in extra parameters:
public void SquareArray(int[] arr, int index)
{
arr[index] *= arr[index];
SquareArray(arr, index + 1);
}How we have an extra variable for incrementing and tracking the index. Think of the index as the i in a for loop, but just with recursion.
Our code isn’t perfect just yet though. Our function will throw an error once the index goes past the end of the array. We need to add a base case to prevent this.
public void SquareArray(int[] arr, int index)
{
if(index >= arr.Length) Console.WriteLine("End of the index. Closing program");
arr[index] *= arr[index];
SquareArray(arr, index + 1);
}We’ve now learned how to look at any plain iterative function call and “recursify” it. Remember to implement recursion think of how you would solve the problem iteratively and use the tricks above to create state.