Algorithm Patterns 101: Two-Pointer

Two pointers is simply an alogorithm pattern that uses multiple pointers to iterate over a collection.

What is a “pointer”? A pointer is just a number that stores where you are at. Almost like a bookmark, it keeps track and indexes the current place you are iterating.

Why do we need pointers? In %99 of everyday development, pointers are useless and abstracted away from you. But in DSA, it is important because we are often trying to sort, filter, traverse, etc. During interviews, employers are going to ask you questions that will require you to create complex for loops where indexes cannot be extracted away.

Where Two-Pointer Shines

• Requirement to find two data elements in an array that satisfy a certain condition
• Data is linear
• Specific range we can identify

Overview

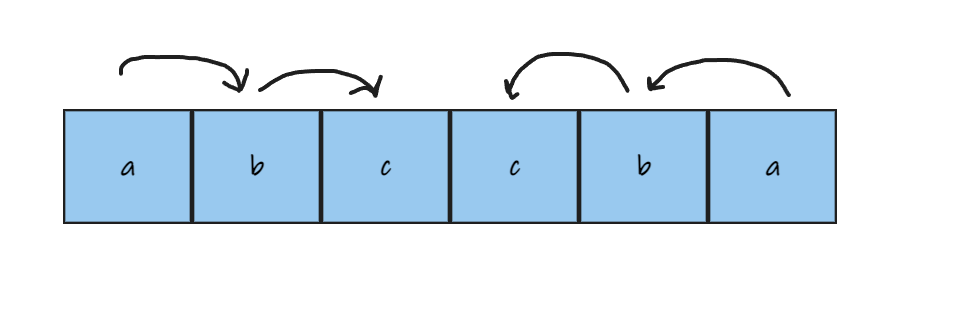
• By using two pointers moving towards the middle, we can use symmetry to our advantage.
• This allows us to compare the elements in a single loop

//Initialize to zero
pointer = 0
arr = [10, 30, 50, 70, 100]
       ^
//Use our newly created pointer variable to point to 0 index
arr[pointer] = arr[0] = 10
//if we initialize to 3, our pointer is now at the 4th spot.
pointer = 3
arr = [10, 30, 50, 70, 100]
                    ^
arr[pointer] = arr[3] = 70

In the code snippet, we initialize a pointer to 0 and use it to point to the 0th index in out input array. If pointer is equal to 3, it will point to the third index.

Valid Palindrome

A palindrome is fancy speak for “this word is the same backwards”. The following are all examples of palindromes:

• civic
• madam
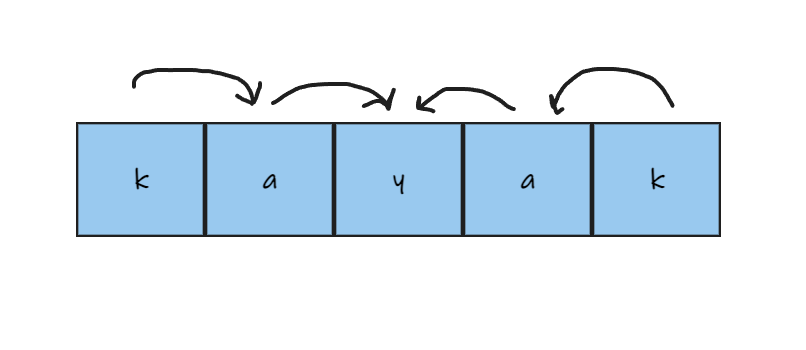
• kayak
• level

In a valid palindrome, the first and last letter of the input must be the same! Followed by the second to first and second to last, etc, etc, etc.

To begin checking we must initialize one pointer on each end.

Step-By-Step Solution

We need to create two pointers.

• The first pointer is at the starting element, while the second is at the end of the string.
• We move the two pointers toward the middle of the string
• At each iteration, we compare each element.
• If we encounter a non-equal pair, return false;

  public static boolean isPalindrome(String s) {

    //Create the pointers. One at starting element. The second at the end.
    int left = 0;
    int right = s.length() - 1;

 

    while (left < right) {
      //If we encounter a non-equal pair, return false
      if (s.charAt(left) != s.charAt(right))
      {
        return false;
      }
      
      //Move the pointers toward the middle of the string
      left = left + 1; // Heading towards the right
      right = right - 1; // Heading towards the left

    }
    // We reached the middle of the string without finding a mismatch, so it is a palindrome.
    return true;
  }

Palindrome Time & Space Complexity

The time complexity is O(n) because we still have to iterate over the entire string. We also get added benefit of (n/2), since pointers are traversing towards the middle.

The space complexity is O(1), since we use constant space to store two indexes.