Valid Mountain Array in Java (Explained Simply)

Essentially, this Leetcode question is asking “do the numbers in an array go up then go down“. It’s called a mountain array because if you draw a line tracing the path of the numbers it will look something like this:

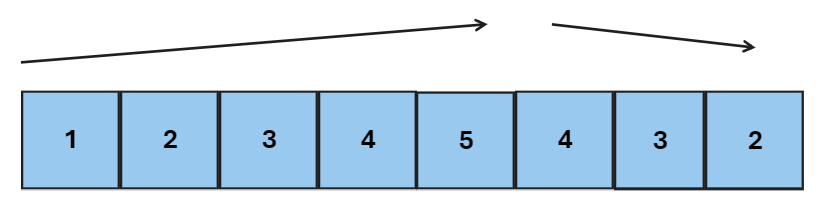
The following conditions must apply:

• Length of the array must be bigger than or equal to 3 (no matter what a valid mountain array cannot be 2)
• There exists some index such that
  • a[0] < a[1] < … < a[i] (fancy algebra for “all the elements until the i are incrementing”)
  • a[i] > a[i + 1] > … > a a[a.size – 1] (fancy algebra for “after the i till the end are decrementing”)

Another way to describe this algorithm is, find if there is an increasing subarray followed by a decreasing subarray.

Step-by-step

First we must consider, how do we check for an increasing sequence?

• We can loop through the array and at each sequence, we check to see if the current element is bigger than the previous. If the above condition fails, we break from the loop.

//Loop over array as long as it's increasing
//We are check for increasing sequences aka increasing part of the mountain
i = 1
while(i < arr.length && arr[i] > arr[i-1]) {
    i+=1;
}
//if loop index didn't move or reach the end, no mountain
if(i == 1 || i == arr.length))
    return false;
//Loop over array starting from the loop index as long as the mountain is going down
while(i < arr.length && a[i] < a[i-1]) {
    i+=1
}

Do we need pointers?

Yes. We need to keep track of where the increasing part of “the mountain” ends, because we need to know where to start check for the downward slope of the mountain.

We could further optimize by returning false if there are no increasing subsequences (aka the mountain is one big slope)

Solution

public boolean validMountainArray(int[] arr) {
    if(arr.length < 3) {
         return false;
    }

    int i = 1;

    while(i < arr.length && arr[i] > a[i-1]) {
        i+=1;
    }

    if(i == 1 || i == arr.length) {
        return false;
    }

    while(i < arr.length && arr[i] < arr[i - 1]) {
        i+=1
    }

    return (i==arr.length)
}